Overview of Material Platform
“Trilogy” of transition-metal kagome materials (A material platform across full spectrum of correlation and topological)
1. Mott Insulators:
ZnCu3(OH)6Cl2, ZnCu3(OD)6Cl2
Quantum spin liquid
Fractionalized spin excitations
doped Mott insulators
frustrated magnetism
2. Magnetic Metals:
Fe3Sn3: FM massive Dirac Fermion
Co3Sn2S2: Magnetic Weyl Semimetal
TbMn6Sn6: FM Chern gap (QAH)
FeSn, FeGe: FM 2D Dirac
Magnetism and CDW oder in FeGe
CoSn, Mn3Sn,…
3. Nonmagnetic Superconducors:
AV3Sb5(A=K, Cs, Rb)=KVS, CVS, RVS new family of CDW
Casecade of symmetry breaking correlated and topo. states.
Universal long-range scaling
The kagome lattice and electronic band structure properties
Tight-binding model
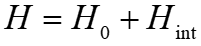
Hopping +Chemical potential
on-site Hubbard inter of scale U0 + nearest neighbor Coulomb inter of scale
tij-the hopping integral: kinetic energy of electrons hopping between neareast-neighbor sites.
cjd-anihilationn operators of electrons on the i site with spin d.
ni,d=cid+cid.
Mn3Sn
The material parameters for the Mn3Sn monalyer Kagome lattice given in (). The in-plane lattice constant as shown in Figure is a = XXX nm, the tight binding parameter is to = XXX meV, which results in vF = XXX x105 m/s. The SOC parameter λ0 ≈ XXX meV, which results in a bandgap Eg ≈ 32 meV and a ratio of
Can I get the single-layer 3d transition-metal-based kagome magnet Mn3Sn succesfully in the 2D limit.
Unravel the atomic and electronic structure of Mn3Sn on Pt(111) or Ag(111) and reveal the compact localized eignestates ingerited from its kagome lattice structure.
Substrate hybridization could largely complicate the band structure. [how to eliminate this point? resemble that of the freestanding one]
The clean Pt(111) or Ag(111) substrate with large terraces was obtained via standard cycles of sputtering and subsequent annealing. During sample growth, high-purity Mn (99.99%) and Sn (99.99%) at a Mn/Sn beam flux ratio of 3:1 (3:0.9?) were codeposited on the Pt substrate held at 30-500 for XXX min. And then annealed surfaces at XXX for 10-60 min.
the intrinsic topological states that potentially host chiral edge modes.
in 2D limit hold geometric fructration
corner-sharing triangles
2D Chern insulator phase on the kagome lattice with the reduction of interlayer hopping in kagome bulk crystals.
non-van der Waals materials
not able to be thinned down to 2D form yet
be exfoliated into atomically single layer but in small flake size and with poor controllarbility
the destructive quantum interference
the unambiguous discoveries of flat band inherited from the kagome lattice.
the direct observation of the compact localized states, i.e., the electronic localization owing to the destructive interference between different sublattices with nearest-neighbour hoppings, is still lacking.
nanoflakes
visulaize the atomic structure and the compact localized eignestates in the Mn3Sn nanoflakes, which manifests the destructive quantum interference in the kagome lattice.
the intrinci Chern quantum phases characterized by the topologicla nontrivial band inversion and chiral edge modes, suggesting the topological origin of the observed edge states.
ine the absence of interlayer electronic hopping
three polymorphs
In each unit cell, three equivalent Mn atoms construct a kagome lattice with one Sn atom centered at the hexagonal hollow site in the same basal plane,
how to control of the stoichiometric ratio and the substrate T.
the codeposition of ~
at a nominal Mn/Sn beam flux ratio of 3
the Mn3Sn single-crystalline nanoflakes grown on Ag(111) or Pt(111) with hexagonal facets and 2 different contrasts.

All the nanoflakes are well aligned to the same orientation
The height profile along the red dashed line in panel reveals two different heights of the nanoflakes, namely 1.94 Å(type-1) and 3.98 Å (type-2) that is close to the c-axis unit of bulk FeGe (4.05Å) indicating the possible growth of 1-UC FeGe. Considering that the height difference between the type-1 and type-2 nanoflakes is very close to a single atomic step of Ag(111), the thinner type-1 nanoflakes are proposed to be 1-UC FeGe sitting on the lower terrace of the Ag(111) substrate.
the height difference between the edge and center shown in the constant current STM line profile is due to the higher local density of states (LDOS) at the edge as discussed below.
The subtle buckling is proposed to arise from weak π bonds and is stabilized via the π–σ interactions among Ge atoms. similar buckling structure has been commonly observed in 2D Xenes (X = Si, Ge, Sn).
The line map of dI/dV across a type-2 FeGe island along the red arrow demonstrates that the edge states are mainly located within a 11A-wide rim along the edges, which can be further spatially resolved in the dI/dV map in ~. Such wide penetration depth of the observed edge states suggests the nontrivial topological nature of the ~. The peak in the dI/dV spectra around 0.1 eV could arise from the flat band residing on the kagome lattice.
The existence of the flat band can be confirmed by the observation of its eignestates, namely the compact localized states at the hexagonal hollow sites of the kagome lattice.
A pronounced resonance with a Fano line shape at EF is robust against the perturation of a vector magnetic field.
geometrical frustration and strong correlation based on the kagome lattice Hubbard model.
electronic frustraction; magnetic frustraction-heavy fermions
kagome lattice localized the electronic wave f like heavy f electrons with heh itinerant condcution sea.
strongly correlated 3d kagome metal/heavy fermison locatied f orbital-strong coulomb interactions and flatband.
Kondo model: the localized moments -itinerant conductive sea-peirodic singlet states.
complex inter-band nature of the nesting
DFT: FSN-incommensurate phase transition
Large areas of these Fermi-surfaces are connected by kb and kx.
Non-coplanar Long Wavelength Magnetism and Charge Order in the Kagome-based Weyl Semimetal Mn3Sn.
A centro-symmetric semi-metal
Interpaly between magnetic order and itinerant electrons lifting kramers degenracy.
The (converse) impacts of relativistic electrons on magentic interactions and the reyslting magnetic orders.
Nesting instabilities for spin and charge with characteristic wave vectors defined by the spacing between Dirac or Weyl points.
Novel quantum phases due to the interpaly and competition between electronic topology, electronn nlocalization and frustrated noncollinear nocoplanar magnetism.
A complex incommensurate modulation of spin, charge and lattice